Lissajous 轨道如何施加脉冲来规避日食?
2022-03-09 18:00:00
最近阅读了一篇介绍 Lissajous 轨道借助不变流形来规避日食的论文,《Eclipse Avoidance for Lissajous Orbits Using Invariant Manifolds》,虽然是 2004 年发表的,但是思路巧妙、方法可行、结果完整。原文涉及到繁琐的数学推导,不过推导过程被作者写的很省略,往往用一句 after some cumbersome algebra 带过,所以读起来是很吃力的。那么这篇笔记就是详细地还原一下那些 cumbersome algebra,供以后参考。
圆型限制性三体问题
动力学方程:
其中,
圆型限制性三体问题有 5 个平动点。其中 3 个在
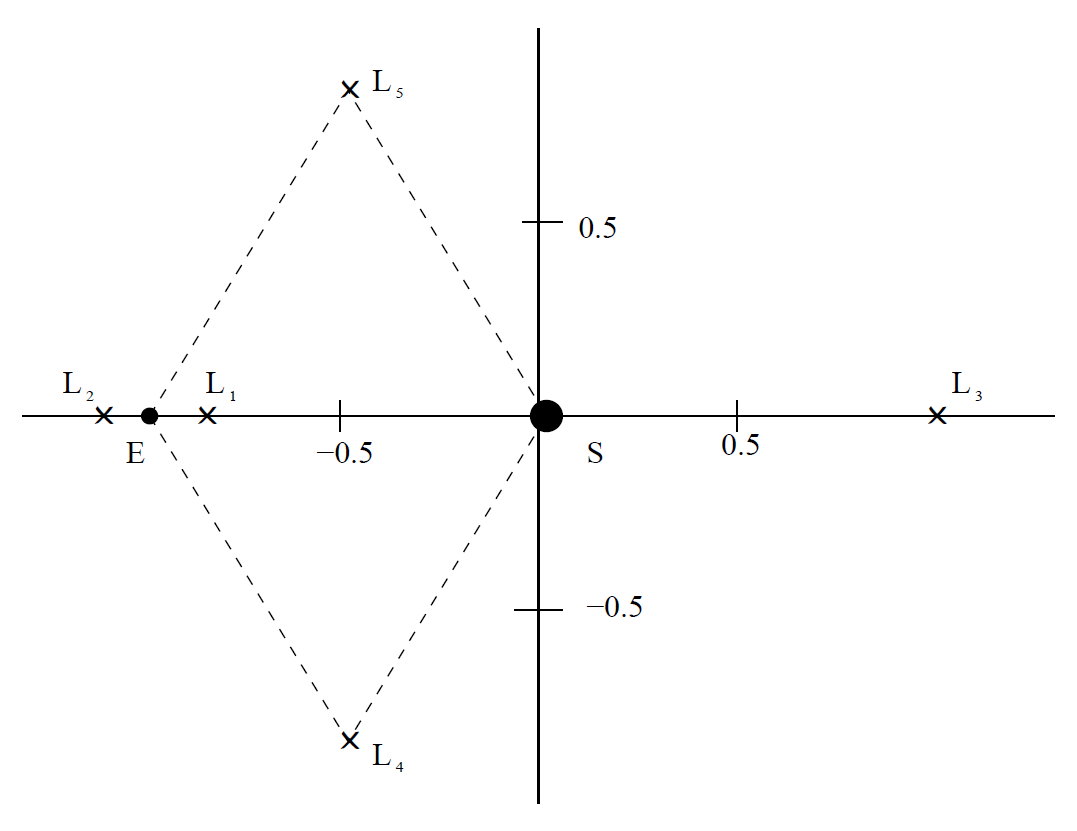
这里只关注这 3 个共线平动点,它们分别满足:
共线平动点附近运动的线性化
记航天器的位置矢量
为了方便书写,给出矢量形式的动力学方程:
而
所以充分利用上述几个
平动点对应的
由于研究平动点附近的运动,所以
另外,由于
因此
经过以上处理,得到了在
把
其中,
把共线平动点满足的条件代入,得到
这里
线性化方程的求解
观察线性微分方程,很显然,
即
方程有 4 个解
因此,
方程有 2 个解
因此,
解的构造
根据常微分方程解的理论,可以把
其中
解得
记
则
求解完毕。
解的变形
把三角函数的项合并:
其中
Lissajous 轨道
选择
三维轨迹如下
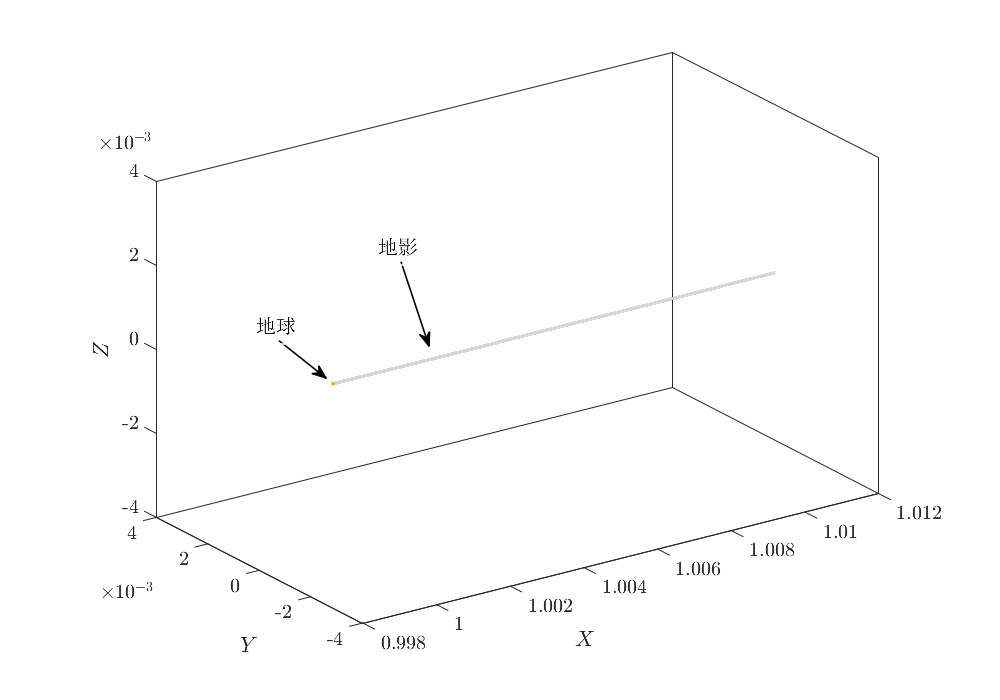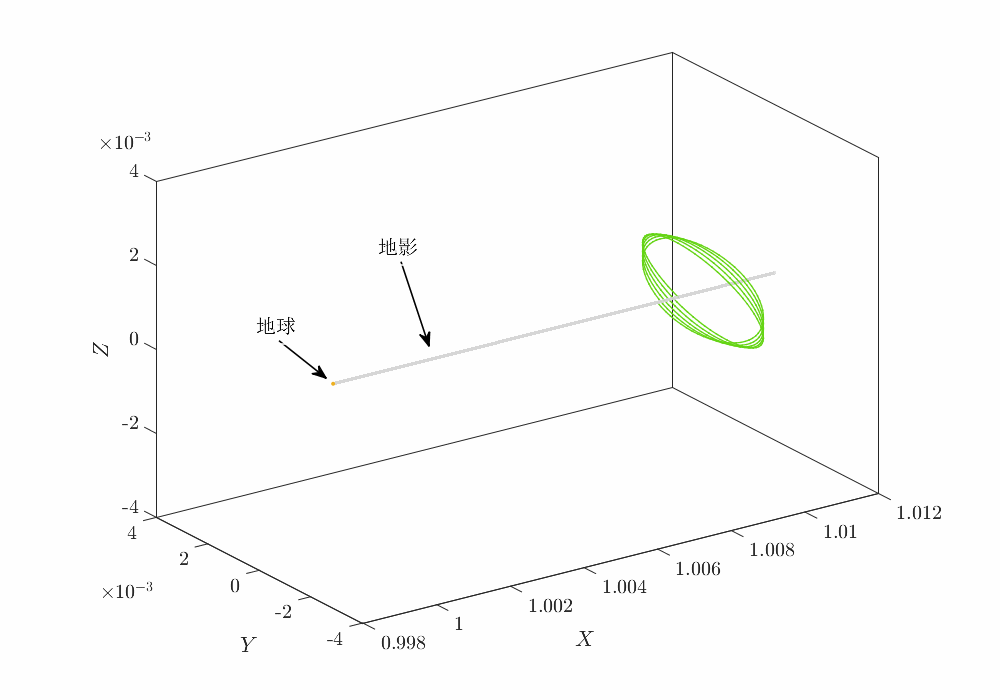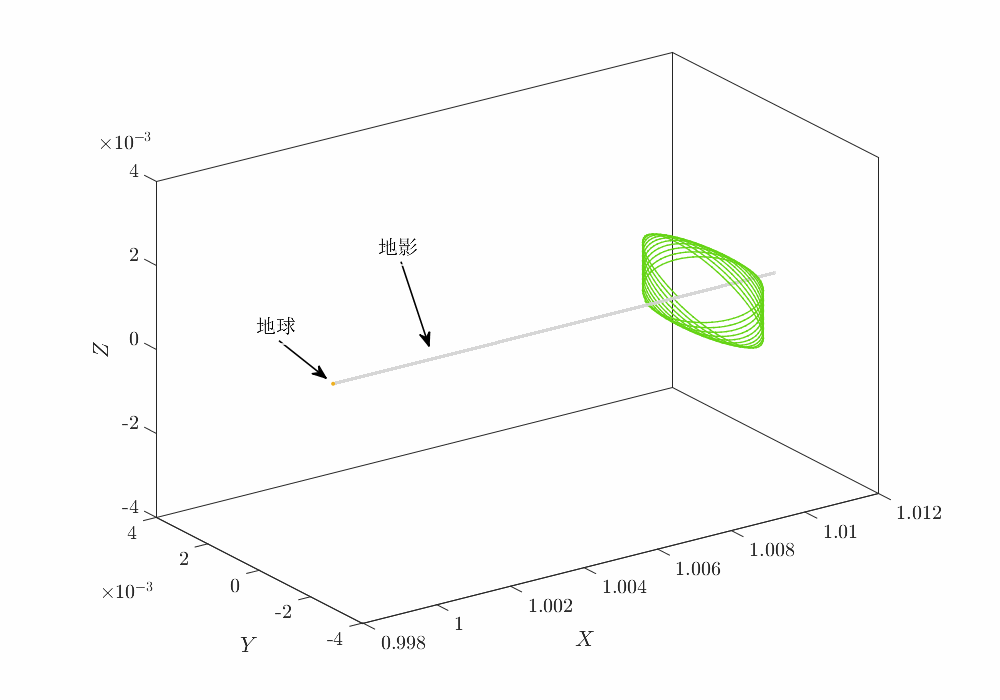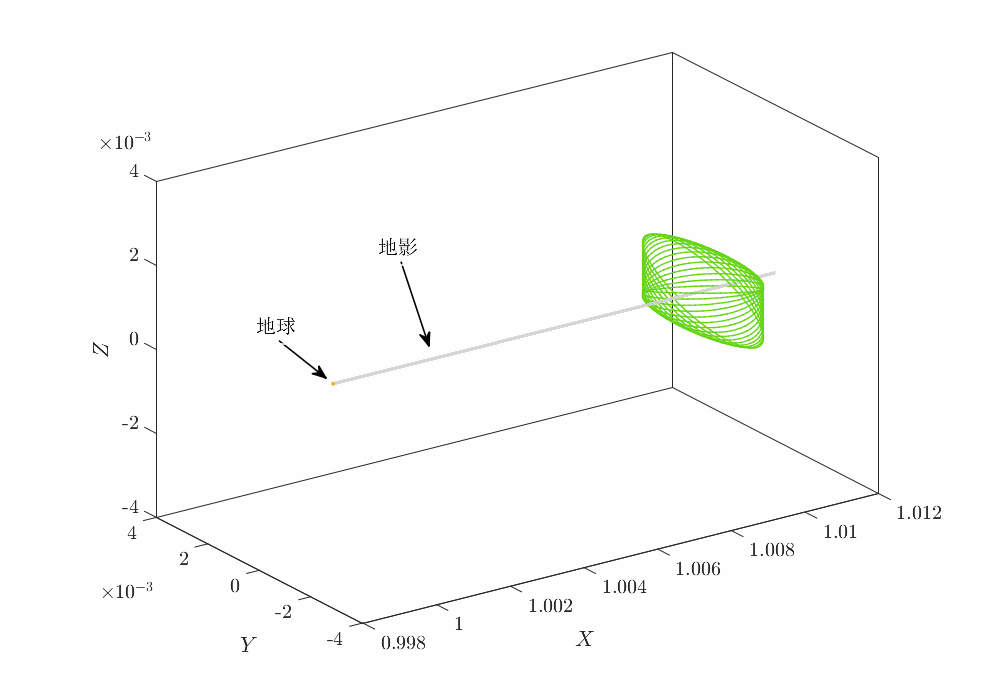
施加
因为
脉冲对振幅的影响
记施加脉冲前的振幅为
作差,得到
解得
故施加脉冲后
据此,可以解出
保持振幅不变
下面考虑施加脉冲却不改变振幅的情况,即
第二个解相当于没有脉冲,振幅当然不会改变,所以舍掉。
振幅不变时相位如何改变
把振幅不变的条件代入
通过对比,可以发现
或者
这意味着:只要设定好相位改变量,就可以确定何时施加脉冲,进而又可以把脉冲的大小确定出来。这就是规避日食的原理。
施加
在时刻
脉冲对振幅的影响
联立求解
太复杂了,借助 Mathematica 求解:

整理一下
记
因为施加脉冲之前,航天器在 Lissajous 轨道上,因此对于
那么以下几个关系成立
进一步
则
上式定量地确定了脉冲
稳定流形
考虑到
因此
变形为
这是由不稳定运动方向的系数
另外,施加脉冲后,如果想要保持上述条件,即
那么必须使得下式成立:
这说明
因为
稳定流形情况下脉冲对振幅的影响
把上述
其中
解得
振幅不变时相位如何改变
下面考虑施加脉冲却不改变振幅的情况,即
备注:和
效仿
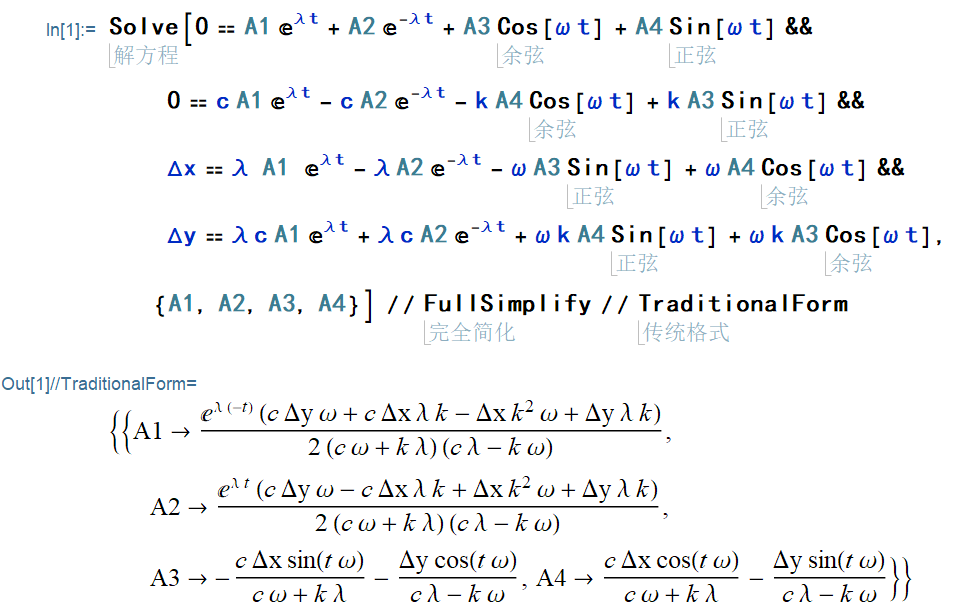
整理一下
把
通过对比,可以发现
或者
只要设定好相位改变量,就可以确定何时施加脉冲,进而可以确定脉冲大小,而脉冲方向是固定的。这就是施加
有效相平面
原文定义了有效相平面的概念,令
以
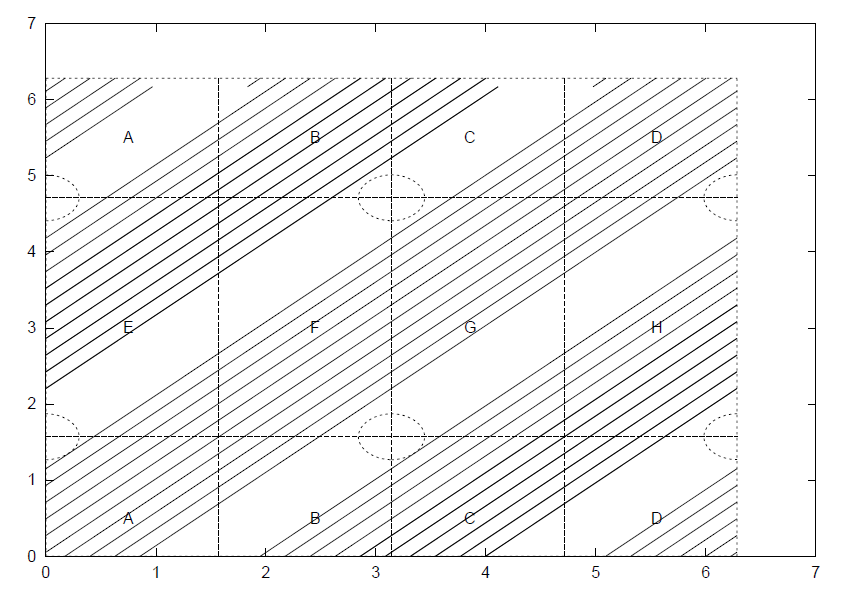
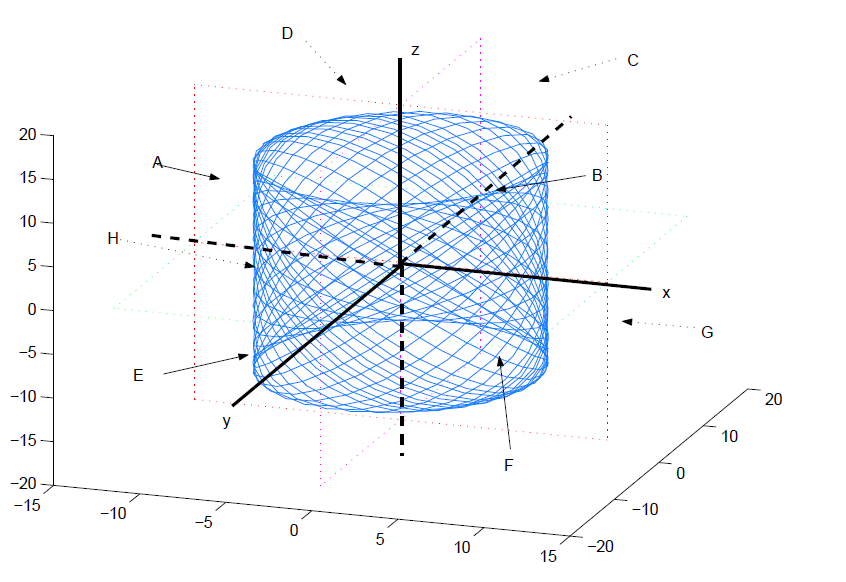
规避日食
通过以上分析,发现施加脉冲可以调整 Lissajous 轨道的相位,且可以不改变其振幅,那么这个特性很容易应用在规避日食上。日食区域可以用下面的形式描述:
因为
所以日食区域的边界就是:
在有效相平面上它是一个椭圆。
下图中,A 代表航天器在有效相平面上的初始位置,如果不干预,它将进入日食区域。通过在 B 处施加
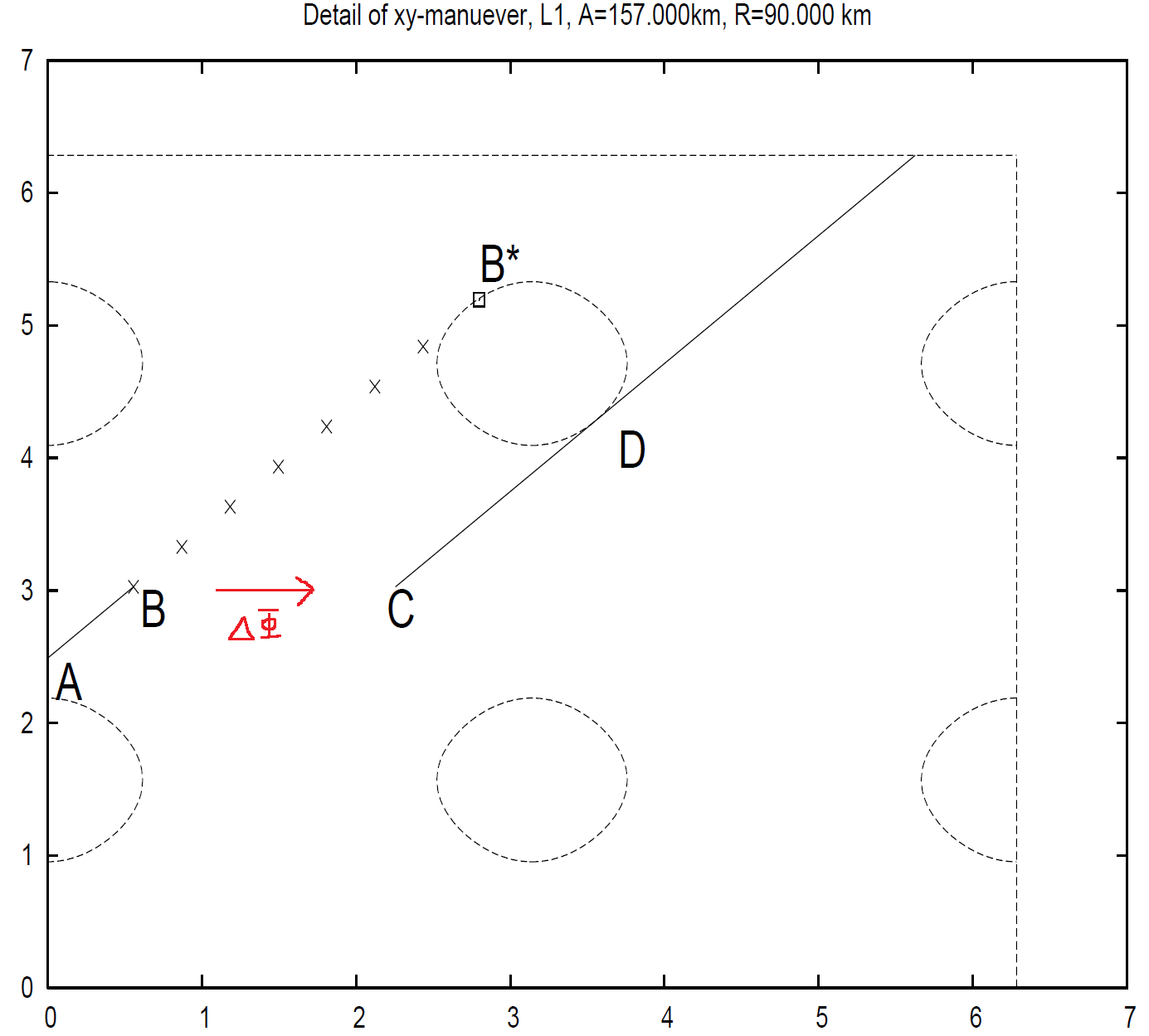
施加
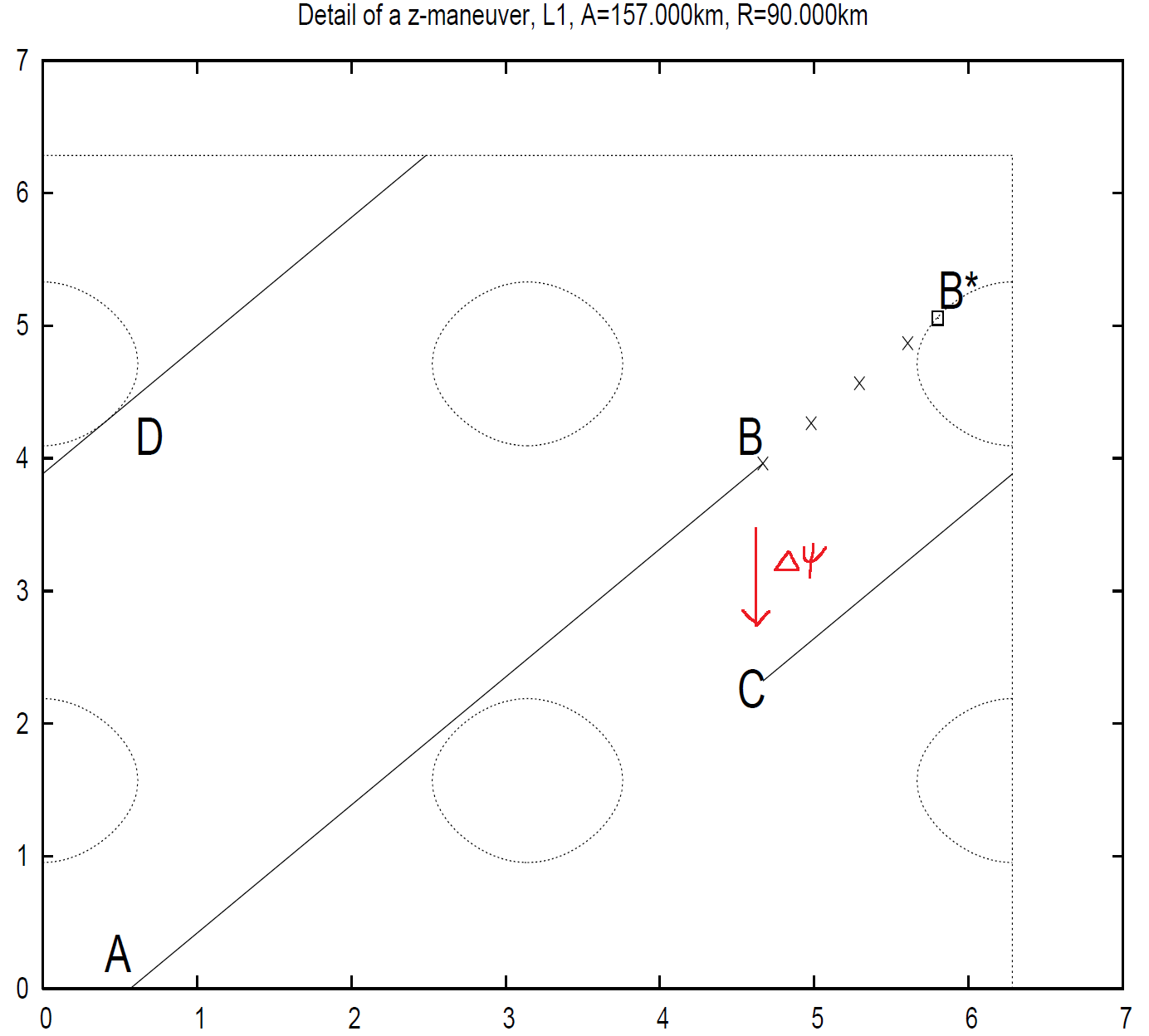
Lissajous 轨道如何施加脉冲来规避日食?